Probabilistic Interpolation of Quantum Rotation Angles
Moving from the 8-bit Nintendo Entertainment System to the 16-bit SNES, unlocked richer virtual worlds due to the increased bits of resolution. Increasing the resolution of electronic systems used to control qubits would similarly further improve the performance of quantum computers.
We can ask, how many bits of resolution are needed to control quantum computers and allow them to perform useful algorithms? Previous attempts to answer this question suggested that to run quantum algorithms with high fidelity, the control systems would need a resolution of at least 12-bits or more. However, high resolution systems require more complex hardware engineering.
To tackle this problem, Bálint Koczor, John Morton, and Simon Benjamin of Quantum Motion, present in Physical Review Letters, a new idea called Probabilistic Angle Interpolation (PAI), a technique that minimises the engineering complexity required of control electronics while achieving comparable performance in the quantum algorithm.
To run a quantum algorithm, hardware platforms need to be able to implement a universal set of gate operations. Gate operations can be regarded as rotations. Most near-term quantum algorithms require that any continuous value of rotation angle must be possible.
However, rotations in real devices are defined and implemented using digital control electronics, meaning that the rotations need be described by a discrete number of values (bits), called the resolution.
In principle, if a quantum computer has access to a small number of (perfectly implemented) angles as native operations, then by applying a suitable sequence of these operations we can actually obtain any rotation we want. But this approach is really only suitable for the fault tolerant era of quantum computing because it makes the circuits ‘deeper’ i.e. more complex and slower to execute.
For nearer term systems, the simple alternative is to have a large number of rotation angles available so that whatever the algorithm needs, can be almost perfectly achieved directly in the hardware by choosing the nearest available angle — but this then comes at the cost of having very high resolution control systems.
PAI offers another approach to this challenge. The technique operates by randomly instructing the control electronics to randomly choose one of three possible rotation angles in each gate operation. The circuit is repeated, and the individual outputs are combined such that on average the exact, desired rotation is obtained.
This approach does mean an increased number of circuit repetitions, but the team prove that their technique achieves the least possible overhead when compared to other well-established techniques.
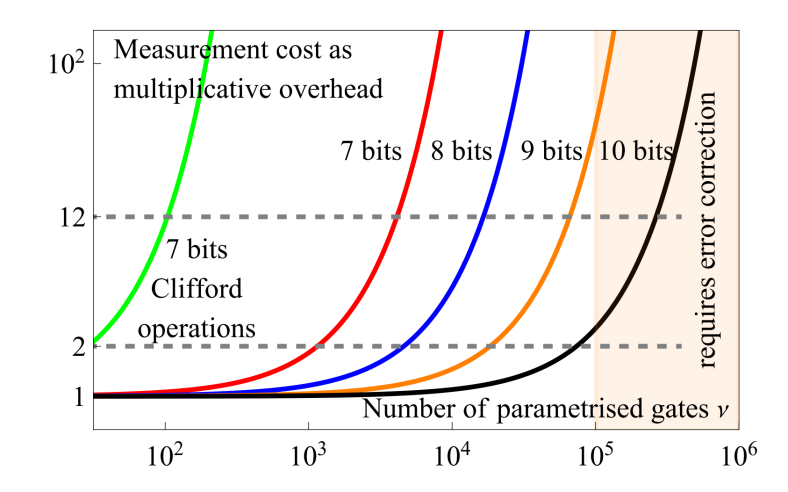
The number of repeated circuits associated with PAI is remarkably modest even with thousands of gates and only 7 bits of resolution available in the control systems. The team expect that this will match the upper requirements of first generation quantum hardware.
According to the team, if PAI is used then future mature generations of quantum computing hardware, expected to be able to execute tens of thousands of quantum gates without error correction, will need no more than 9 bits of resolution in their control systems.
Using PAI the team show that anyone can effectively upgrade a device that can only realise discrete rotation angles to a device that can perform arbitrary, continuous rotation angles – and crucially, this is achieved without increasing circuit depths.

